METODE NEWTON RAPSON

Metode Newton-Raphson adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) mempunyai turunan. Metode ini dianggap lebih mudah dari Metode Bagi-Dua (Bisection Method) karena metode ini menggunakan pendekatan satu titik sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar sebenarnya, maka semakin cepat konvergen ke akarnya.

 

Prosedur Metode Newton :

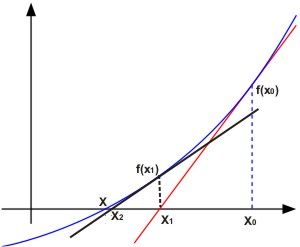
menentukan x sebagai titik awal, kemudian menarik garis lurus (misal garis l) yang menyinggung titik f(x). Hal ini berakibat garis l memotong sumbu – x di titik x₁. Setelah itu diulangi langkah sebelumnya tapi sekarang x₁ dianggap sebagai titik awalnya. Dari mengulang langkah-langkah sebelumnya akan mendapatkan x₂, x₃, … x_n dengan x_n yang diperoleh adalah bilangan riil yang merupakan akar atau mendekati akar yang sebenarnya.

Perhatikan gambar diatas untuk menurunkan rumus Metode Newton-Raphson

persamaan garis l : y – y = m(x – x)

y – f(x) = f’(x)(x – x)

x₁ adalah perpotongan garis l dengan sumbu – x

0 – f(x) = f’(x)(x₁ – x)

y = 0 dan x = x₁ maka koordinat titik (x₁, 0)

–  = (x₁ – x)

x₁ = x –

x₂ = x₁ –

.

.

.

x_n = x_n-1- untuk n = 1, 2, 3, …

Contoh :

Tentukan akar dari persamaan 4x³ – 15x² + 17x – 6 = 0 menggunakan Metode Newton-Raphson.

Penyelesaian :

f(x) = 4x³ – 15x² + 17x – 6

f’(x) = 12x² – 30x + 17

iterasi 1 :

ambil titik awal x = 3

f(3) = 4(3)³ – 15(3)² + 17(3) – 6 = 18

f’(3) = 12(3)² – 30(3) + 17 = 35

x₁ = 3 – 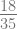= 2.48571

iterasi 2 : 

f(2.48571) = 4(2.48571)³ – 15(2.48571)² + 17(2.48571) – 6 = 5.01019

f’(2.48571) = 12(2.48571)² – 30(2.48571) + 17 = 16.57388

x₂ = 2.48571 – 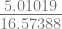= 2.18342

iterasi 3 :

f(2.18342) = 4(2.18342)³ – 15(2.18342)² + 17(2.18342) – 6 = 1.24457

f’(2.18342) = 12(2.18342)² – 30(2.18342) + 17 = 8.70527

x₃ = 2.18342 – 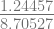= 2.04045

iterasi 4 :

f(2.04045) = 4(2.04045)³ – 15(2.04045)² + 17(2.04045) – 6 = 0.21726

f’(2.04045) = 12(2.04045)² – 30(2.04045) + 17 = 5.74778

x₄ = 2.04045 – 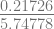= 2.00265

iterasi 5 :

f(3) = 4(2.00265)³ – 15(2.00265)² + 17(2.00265) – 6 = 0.01334

f’(2.00265) = 12(2.00265)² – 30(2.00265) + 17 = 5.04787

x₅ = 2.00265 – 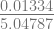= 2.00001

iterasi 6 :

f(2.00001) = 4(2.00001)³ – 15(2.00001)² + 17(2.00001) – 6 = 0.00006

f’(2.00001) = 12(2.00001)² – 30(2.00001) + 17 = 5.00023

x₆ = 2.00001 – 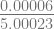= 2.00000

iterasi 7 :

f(2) = 4(2)³ – 15(2)² + 17(2) – 6 = 0

jika disajikan dalam tabel, maka seperti tabel dibawah ini.

n	xn	f(xn)	f’(xn)
1 2 3 4 5 6	3 2.48571 2.18342 2.04045 2.00265 2.00001 2.00000	18 5.01019 1.24457 0.21726 0.01334 0.00006 0.00000	35 16.57388 8.70527 5.74778 5.04787 5.00023 5.00000

karena pada iteasi ketujuh f(x₆) = 0 maka akar dari persamaan tersebut adalah x =2.
www.iaincirebon.ac.id